문제 바로가기 => 가장 긴 증가하는 부분 수열
🔒 문제
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에
가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
⌨ 입력
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.
둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)
🖨 출력
첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.
📚 예제
6
10 20 10 30 20 50
Ex)
4📌 풀이
1번 풀이 (O(n^2))
*dp[ N ] = 0 ~ N - 1 인덱스에 저장된 갑 중 N번째 인덱스 값보다 작은 값들의 개수 * 로 값을 저장할 것이다.
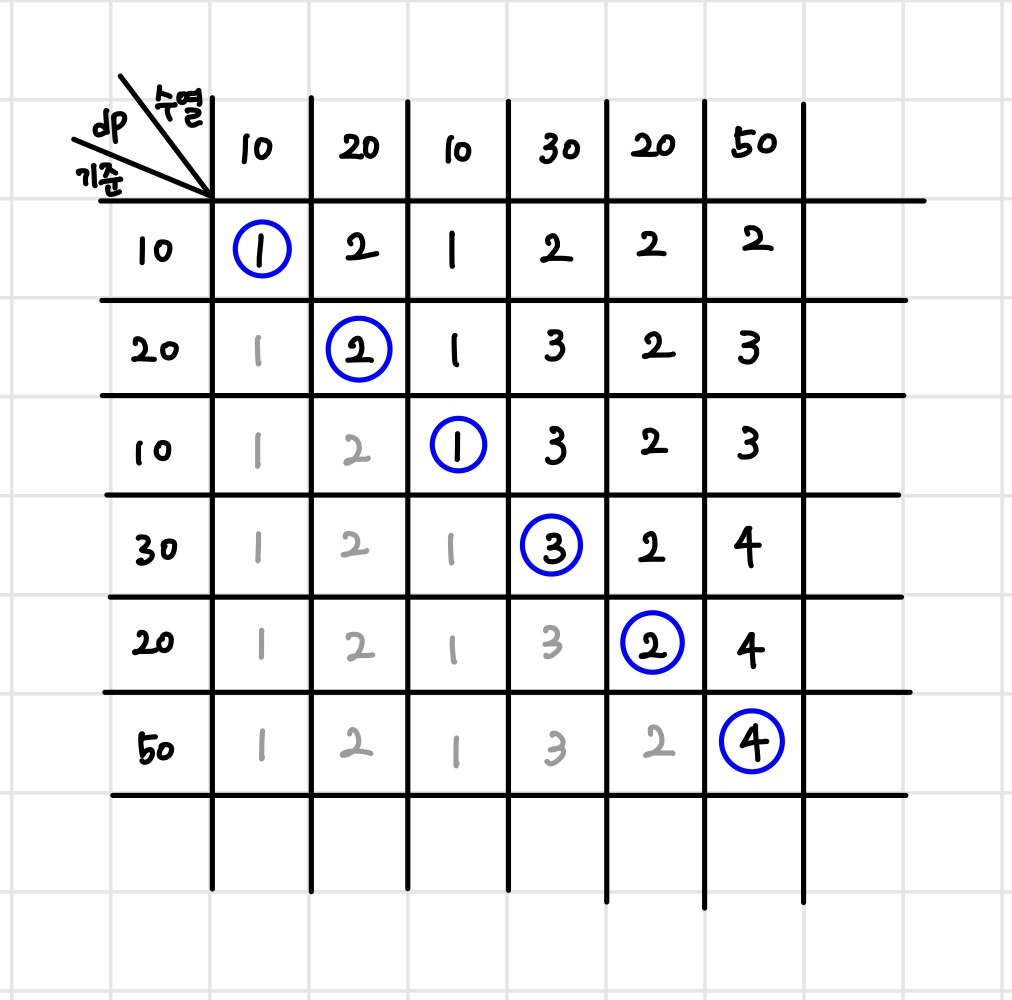
위 그림의 각 행은 시행 할 때 마다 dp[ N ]에 저장되는 값들을 보여주는 것이다.
맨 왼쪽 열은 각 시행에서 비교할 값들 이다.
즉 맨 오른쪽 행은 각 시행에서 비교 기준이 될 값이고, 맨 위의 열은 각 시행에서 비교될 값들을 적은 것이다.
예를들어 설명을 해보자.
입력받은 수열 arr[i] 가 기준이 된다고 하자.
그럼 우리는 k + 1 번째 인덱스부터 N - 1에 저장된 값까지 비교를 할 것이다.
k + 1 ≤ j ≤ N - 1 라고 하자.
만약 arr[i] < arr[j] 라면
dp[j] = max(dp[i] + 1, dp[j]) 이다.
dp[j] = max(dp[i] + 1, dp[j])을 하는 이유는, 수열 중 중복되는 값들이 존재할 수 있기 때문에, 중복 카운팅이 되는 것을 방지하기 위해서 이다.
그리고 자기자신도 길이에 포함되기 때문에 dp를 처음 만들 때, 1을 넣어주는 것이 좋다.
2번째 풀이 (O(n^3))
두번째 풀이는 이차원 배열로 풀었다. 확실히 시간 복잡도가 너무 커져서 python3로는 시간 초과가 떴고, pypy로 간신히 통과를 했다.
지금보니까 굉장히 비효율의 극치인 것 같다.
이것과 관련된 풀이는 나중에 수정해서 올리겠다. (오늘밤이나 새벽에 시간되면)
🔑 python 코드 1
import sys
N = int(sys.stdin.readline())
arr = [int(x) for x in sys.stdin.readline().split()]
dp = [1 for _ in range(N)]
for i in range(N):
for j in range(i + 1, N):
if(arr[j] > arr[i]):
dp[j] = max(dp[i] + 1, dp[j])
print(max(dp))🔑 python 코드 1
import sys
N = int(sys.stdin.readline())
arr = [int(x) for x in sys.stdin.readline().split()]
dp = [[1 for _ in range(N)] for _ in range(N)]
for i in range(N):
for j in range(i + 1, N):
for k in range(i, j):
if(arr[k] < arr[j]):
dp[i][j] = max(dp[i][j], dp[i][k] + 1)
print(max(max(dp)))'BAEKJOON > 알고리즘' 카테고리의 다른 글
| [BOJ] 2631번 : 줄세우기 (0) | 2023.02.07 |
|---|---|
| [BOJ] 9251번 : LCS (0) | 2023.02.07 |
| [BOJ] 1562번 : 계단 수 (4) | 2023.01.01 |
| [BOJ] 10844번 : 쉬운 계단 수 (0) | 2022.12.30 |
| [BOJ] 1149번 : RGB거리 (Python) (0) | 2022.12.30 |