🔒 문제
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

⌨ 입력
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
🖨 출력
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
📚 예제
Ex1)
2
2Ex2)
9
55📌 풀이
고등학교 때 풀던 확통 문제가 생각나는 문제이다. 수학 문제를 푸는 기분이었다.
dp 행렬에 직사각형의 채우는 방법의 수를 저장 할 것이다.
따라서 dp[가로 길이]로 행렬을 만들어준다
- 가로 길이가 1이면
dp[0] = 1이다.

- 가로 길이가 2이면
dp[1] = 2이다.

- 가로 길이가 3이상이면 dp를 식으로 나타 낼 수 있다.
가로가 3 이상인 직사각형을 만드는 방법은 크게 2가지가 있다.
1) dp[n-1] 에 세로의 직사각형 붙이기
2) dp[n-1] 에 세로의 직사각형 2개나, 가로의 직사각형들 붙이기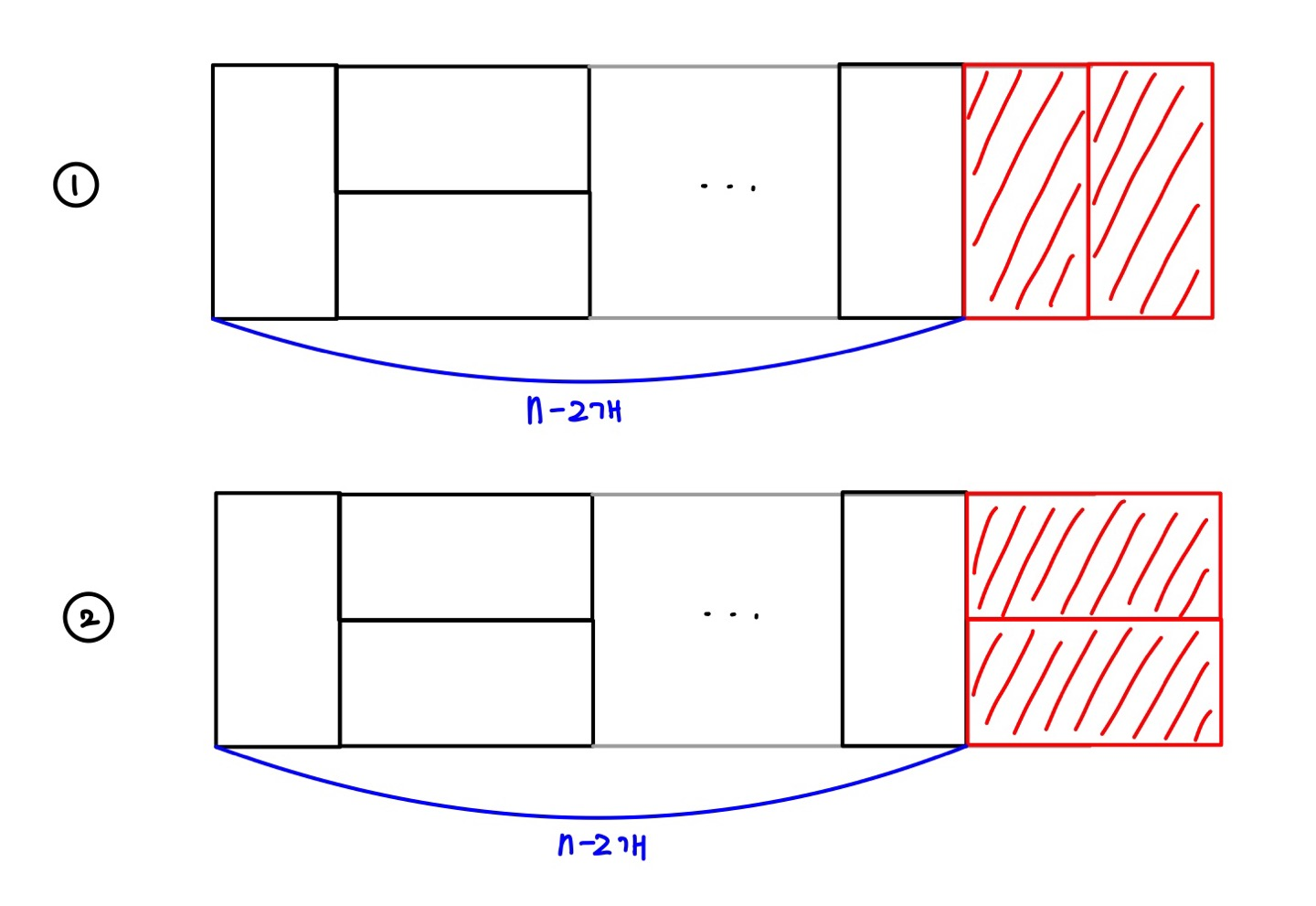
하지만 2) - 1의 경우의 수는 1) 방법의 부분 집합이기 때문에,
1)과 2)-2만 사용하여 dp[n]을 구한다.
즉,
dp[n] = dp[n-1] + dp[n-2] (n >= 3)
로 나타낼 수 있다.
정리하자면,
1. n == 1
dp[0] = 1
2. n == 2
dp[1] = 2
3. n >= 3
dp[n] = dp[n-1] + dp[n-2]
으로 나타낼 수 있다.
🔑 python 코드
import sys
N = int(sys.stdin.readline())
dp = [0 for _ in range(N)]
if(N==1):
dp[0] = 1
else:
dp[0] = 1
dp[1] = 2
for i in range(2,N):
dp[i] = (dp[i-1]+dp[i-2])%10007 #문제에서 나누라 함
print(dp[N-1])'BAEKJOON > 알고리즘' 카테고리의 다른 글
| [BOJ] 1562번 : 계단 수 (4) | 2023.01.01 |
|---|---|
| [BOJ] 10844번 : 쉬운 계단 수 (0) | 2022.12.30 |
| [BOJ] 1149번 : RGB거리 (Python) (0) | 2022.12.30 |
| [BOJ] 1932번 : 정수 삼각형 (Python) (0) | 2022.12.30 |
| [BOJ] 1463번 : 1로 만들기 (Python) (0) | 2022.12.30 |